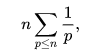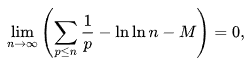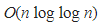에라토스테네스의 체

작성일 | In

에라토스테네스의 체란?

소수를 찾는 간단한 알고리즘이다. 아주 간단하지만, 무시할 수 없는 점은 비교적 빠르게 동작한다는 데에 있다.

현대 암호의 근간을 이루는 소수를 쉽고 빠르게(?) 찾을수 있는 방법인 것이다.

조금 이해하기 쉬운 버전의 의사코드로는 아래와 같다.

1
2
3
4
5
6
A[2 ~ N] = false
I가 N 보다 작으면 반복한다.
    배열에서 값이 false인 가장 작은 수를 I로 택하자. 이 수는 소수이다.
    모든 I의 배수 X에 대해서
        A[X] = true
I로 택해진 수와 배열에서 값이 false로 남아있는 수는 모두 소수이다.

최적화하기(1): 시작 범위 줄이기

위의 의사코드를 조금 더 빠르게 바꿔 볼 수 있다. 먼저 모든 I의 배수 X란 부분을 바꿔 보자.

모든 I의 배수 X를 찾아 A[X] 를 true로 대입하는 부분인데,

잘 생각해 보면 이미 true로 대입되어 있는 부분을 또 대입할 필요가 없다는 사실을 알 수 있다.

즉 모든 I의 배수를 I*I보다 크거나 같은 모든 I의 배수로 바꿔 줄 수 있다.

예제

예를 들어서 생각해보자. 5의 배수를 가정하면 5*5 보다 작은 5의 배수는 5*1, 5*2, 5*3, 5*4이다.

5*1은 I이므로 A[I] 는 true이다. 5*2, 5*4의 경우에는 I=2일때 이미 true로 바뀌었을 것이다.

또 5*3은 I=3일때 true로 바뀌었을 것이다.

즉 I의 배수 X를 X = I * N으로 나타내면, N이 I보다 작은 모든 경우는 이미 true로 체크되어 있는 것이다.

그러므로 의사코드를 바꿀 수 있다.

1
2
3
4
5
6
A[2 ~ N] = false
I가 N 보다 작으면 반복한다.
    배열에서 값이 false인 가장 작은 수를 I로 택하자. 이 수는 소수이다.
    I*I보다 크거나 같은 모든 I의 배수 X에 대해서
        A[X] = true
I로 택해진 수와 배열에서 값이 false로 남아있는 수는 모두 소수이다.

최적화하기(2): 끝 범위 줄이기

이제 끝 범위인 I가 N보다 작으면 반복 부분을 살펴보자.

결론부터 말하자면 이 부분은 I*I가 N보다 작으면 반복 으로 바꿀 수 있다.

(1)에서 찾은 원리와 연관되는데, I*I가 N보다 큰 경우는 탐색을 시작하는 부분이 N을 넘어가 버린다. 즉 탐색 자체가 무의미 해 진다.

이를 의사코드로 최종적으로 바꿔보면 아래와 같다.

1
2
3
4
5
6
A[2 ~ N] = false
I*I가 N 보다 거나 같으면 반복한다.
    배열에서 값이 false인 가장 작은 수를 I로 택하자. 이 수는 소수이다.
    I*I보다 크거나 같은 모든 I의 배수 X에 대해서
        A[X] = true
I로 택해진 수와 배열에서 값이 false로 남아있는 수는 모두 소수이다.

이를 c++로 바꾸면 아래와 같다.

1
2
3
4
5
6
A[N+1] = {0,};

for (int i = 2; i * i <= N; i++)
    if (!A[i])
        for(int j = i*i; j <= N; j += i)
            A[j] = 1;

시간 복잡도 계산

결국 위의 문제는 어떤 소수 p에 대해서 N보다 작은 p의 배수의 개수만큼 시간이 걸린다.

메르텐스의 제 2정리를 이용하면 된다고 하는데, 증명은 필자도 모른다. 위키백과를 참고하자.

이제 n이 매우 커지면 ln(ln(N)) 은 M보다 커지므로, 양변에 N을 곱해 아래와 같이 정리해 볼 수 있다.

이는 생각보다 매우 빠른 시간복잡도인데, N = 1e9가 되어도 ln(ln(N))의 값은 겨우 3이다.

결국 알고리즘 문제에서는 거의 O(N)으로 풀린다고 생각해도 무방한 알고리즘이 된다.